DOE Fundamentals Handbook - Mathematics $17.95

The Mathematics handbook includes a review of introductory mathematics (i.e. addition, subtraction, multiplication and division involving whole numbers, decimals, fractions, exponents and radicals) and the concepts and functional use of algebra, geometry, trigonometry and calculus. Word problems, equations, calculations and practical exercises that require the use of each of the mathematical concepts are also presented. This book will provide YOU with a foundation for performing basic mathematical calculations and understanding the significance of things like quadratic equations, the Pythagorean Theorem, logarithms and trigonometric functions of sine, cosine, tangent, cotangent, secant and cosecant.
The Mathematics handbook presents more than enough information to provide the reader with a fundamental knowledge level sufficient to understand advanced theoretical concepts presented in many other subject areas, including all of the sciences, statistical use of data and all those other realms of life that our parents and teachers told us way back when that we would need math for some day… This book is a Godsend for undergraduate students preparing for the GRE’s who are in desperate need of a wonderfully clear, concise and FUNDAMENTAL breakdown of mathematics. It is also particularly useful for anyone in any field that finds their math skills woefully inadequate or even just rusty to the point of irritation

 

 

 

 

 

 

 

 

 

 

 

DOE FUNDAMENTALS HANDBOOK MATHEMATICS

VOLUMES 1-2

 

 

 

The Department of Energy (DOE) Fundamentals Handbooks consist of ten academic subjects, which include Mathematics; Classical Physics; Thermodynamics, Heat Transfer, and Fluid Flow; Instrumentation and Control; Electrical Science; Material Science; Mechanical Science; Chemistry; Engineering Symbology, Prints, and Drawings; and Nuclear Physics and Reactor Theory. The handbooks were first published as Reactor Operator Fundamentals Manuals in 1985 for use by DOE category A reactors. The subject areas, subject matter content, and level of detail of the Reactor Operator Fundamentals Manuals were determined from several sources and prepared by the DOE Training Coordination Program. Each handbook contains an abstract, a foreword, an overview, learning objectives, and text material, and is divided into modules.

The Mathematics Fundamentals Handbook was developed to assist nuclear facility operating contractors provide operators, maintenance personnel, and the technical staff with the necessary fundamentals training to ensure a basic understanding of mathematics and its application to facility operation. The handbook includes a review of introductory mathematics and the concepts and functional use of algebra, geometry, trigonometry, and calculus. Word problems, equations, calculations, and practical exercises that require the use of each of the mathematical concepts are also presented. This information will provide you with a foundation for understanding and performing basic mathematical calculations that are associated with various DOE nuclear facility operations. The Mathematics handbook presents more than enough information to provide the reader with a fundamental knowledge level sufficient to understand the advanced theoretical concepts presented in other subject areas, and to better understand basic system and equipment operations.

The Mathematics handbook consists of five modules that are contained in two volumes. The following is a brief description of the information presented in each module of the handbook.

 

 

 

 

 

 

 

Volume 1 of 2

 

Module 1 - Review of Introductory Mathematics

-Explanation- This module describes the concepts of addition, subtraction, multiplication, and division involving whole numbers, decimals, fractions, exponents, and radicals. A review of basic calculator operation is included.

Addition and Subtraction of Fractions

When two or more fractions have the same denominator, they are said to have a common denominator. The rules for adding fractions with a common denominator will first be explored. Consider the example.

3/8 + 1/8 = ____

First of all, the fraction 3/8 means three 1/8 segments, i.e. 3 = 3 x 1/8 Looking at this as the addition of pie segments: It is obvious that three of these segments (1/8) plus one of these segments (1/8) equal four of these segments (1/8).

This graphic illustration can be done for any addition of fractions with common denominators. The sum of the fractions is obtained by adding the numerators and dividing this sum by the common denominator.

 

 

TERMINOLOGY

Summary

CALCULATOR OPERATIONS

FOUR BASIC ARITHMETIC OPERATIONS

Calculator Usage, Special Keys
The Decimal Numbering System
Adding Whole Numbers
Subtracting Whole Numbers
Multiplying Whole Numbers
Dividing Whole Numbers
Hierarchy of Mathematical Operations
Summary

AVERAGES

Average Value
Summary

FRACTIONS

Proper and Improper Fractions
Equivalent Fractions
Addition and Subtraction of Fractions
Least Common Denominator Using Primes
Addition and Subtraction
Multiplication
Division
Summary

DECIMALS

Fraction to Decimal Conversion
Decimal to Fraction Conversion
Addition and Subtraction of Decimals
Multiplying Decimals
Dividing Decimals
Rounding Off
Summary

SIGNED NUMBERS

Calculator Usage, Special Keys
Addition
Subtraction
Multiplication
Division
Summary

SIGNIFICANT DIGITS

Calculator Usage, Special Keys
Significant Digits

Summary

PERCENTAGES

Calculator Usage, Special Keys
Changing Decimals to Percent
Changing Common Fractions and Whole Numbers to Percent
Changing a Percent to a Decimal
Percent Differential
Ratio
Summary

EXPONENTS

Calculator Usage, Special Keys
Exponents
Basic Rules for Exponents
Zero Exponents
Negative Exponents
Fractional Exponents
Summary

SCIENTIFIC NOTATION

Calculator Usage
Writing Numbers in Scientific Notation
Converting Scientific Notation to Integers
Addition
Subtraction
Multiplication
Division
Summary

RADICALS

Calculator Usage, Special Keys
The Radical
Simplifying Radicals
Addition and Subtraction
Multiplication
Division
Dissimilar Radicals
Changing Radicals to Exponents
Changing Exponents to Radicals
Summary

Appendix A

TI-3- Calculator Keypad Layout

Module 2 - Algebra

-Explanation- This module describes the concepts of algebra including quadratic equations and word problems.

 

 

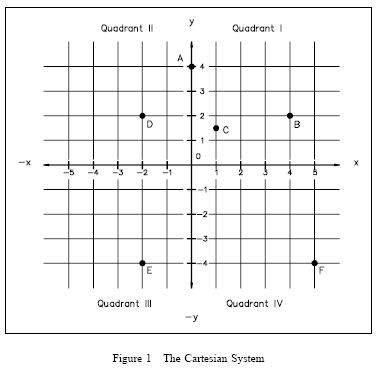
The Cartesian Coordinate System

The Cartesian Coordinate System, also known as the rectangular coordinate system, consists of two number scales, called the x-axis (at y = 0) and the y-axis (at x = 0), that are perpendicular to each other. Each scale is a number line drawn to intersect the other at zero. The zero point is called the origin. The divisions along the scales may be any size, but each division must be equal. Figure 1 shows a rectangular coordinate system. The axes divide the coordinate system into four regions called quadrants. Quadrant I is the region above the x-axis and to the right of the y-axis. Quadrant II is the region above the x-axis and to the left of the y-axis. Quadrant III is the region below the x-axis and to the left of the y-axis. Quadrant IV is the region below the x-axis and to the right of the y-axis.

 

 

 

 

 

 

 

 

 

 

 

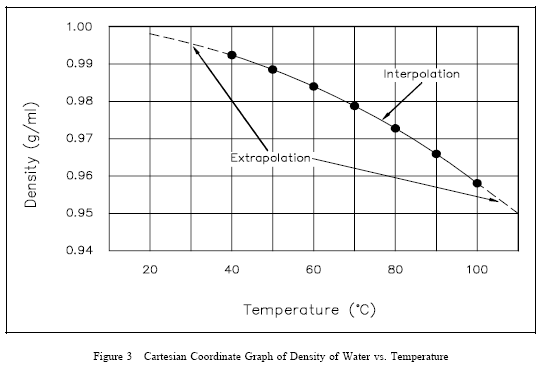
Graphs are convenient because, at a single glance, the major features of the relationship between the two physical quantities plotted can be seen. In addition, if some previous knowledge of the physical system under consideration is available, the numerical value pairs of points can be connected by a straight line or a smooth curve. From these plots, the values at points not specifically measured or calculated can be obtained. In Figures 2 and 3, the data points have been connected by a straight line and a smooth curve, respectively. From these plots, the values at points not specifically plotted can be determined. For example, using Figure 3, the density of water at 65°C can be determined to be 0.98 g/ml. Because 65°C is within the scope of the available data, it is called an interpolated value. Also using Figure 3, the density of water at 101 °C can be estimated to be 0.956 g/ml. Because 101 °C is outside the scope of the available data, it is called an extrapolated value. Although the value of 0.956 g/ml appears reasonable, an important physical fact is absent and not predictable from the data given. Water boils at 100°C at atmospheric pressure. At temperatures above 100°C it is not a liquid, but a gas. Therefore, the value of 0.956 g/ml is of no significance except when the pressure is above atmospheric.

This illustrates the relative ease of interpolating and extrapolating using graphs. It also points out the precautions that must be taken, namely, interpolation and extrapolation should be done only if there is some prior knowledge of the system. This is particularly true for extrapolation where the available data is being extended into a region where unknown physical changes may take place.

 

 

 

 

 

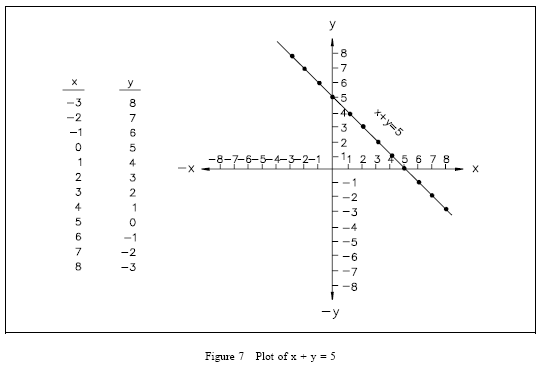
Graphing Equations

Algebraic equations involving two unknowns can readily be shown on a graph. Figure 7 shows a plot of the equation x + y = 5. The equation is solved for corresponding sets of values of x and y that satisfy the equation. Each of these points is plotted and the points connected. The graph of x + y = 5 is a straight line.

The x-intercept of a line on a graph is defined as the value of the x-coordinate when the y-coordinate is zero. It is the value of x where the graph intercepts the x-axis. The y-intercept of a graph is defined as the value of the y-coordinate when the x-coordinate is zero. It is the value of y where the graph intercepts the y-axis. Thus, the x-intercept of the graph of x + y = 5 is +5. For a linear equation in the general form ax + by = c, the x-intercept and y-intercept can also be given in general form.

 

 

 

 

 

 

 

 

 

 

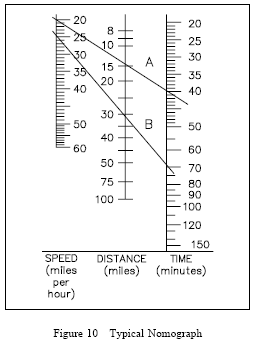
Nomographs

A nomograph is a device used to relate the physical quantities in such a way that the value of an unknown quantity can be determined given the values of the other related quantities. Nomographs normally involve the relationship among three physical quantities. The scales are located in such a way that, when a straight line is drawn between the values of the known quantities on their respective scales, the line crosses the value of the unknown quantity on its scale. Figure 10 is a typical nomograph that relates the distance traveled, the average speed, and the time traveled. It should be noted that, as with any graphical representation, the values determined are only approximations.

 

 

 

 

 

 

 

 

ALGEBRAIC LAWS

Algebraic Laws
Summary

LINEAR EQUATIONS

Solutions to Algebraic Equations
Algebraic Equations
Types of Algebraic Equations
Linear Equations
Solving Fractional Equations
Ratio and Proportion
Summary

QUADRATIC EQUATIONS

Types of Quadratic Equations
Solving Quadratic Equations
Taking Square Root
Factoring Quadratic Equations
The Quadratic Formula
Summary

SIMULTANEOUS EQUATIONS

Solving Simultaneous Equations
Summary

 WORD PROBLEMS

Basic Approach to Solving Algebraic Word Problems
Steps for Solving Algebraic Word Problems
Word Problems Involving Money
Problems Involving Motion
Solving Word Problems Involving Quadratic Equations
Summary

LOGARITHMS

Calculator Usage, Special Keys
Introduction
Definition
Log Rules
Common and Natural Logarithms
Anti-Logarithms
Natural and Common Log Operations
Summary

GRAPHING

The Cartesian Coordinate System
Cartesian Coordinate Graphs
Logarithmic Graphs
Graphing Equations
Nomographs
Summary

SLOPES

Slope
Summary

INTERPOLATION AND EXTRAPOLATION

Definitions
Interpolation and Extrapolation
Summary

 

Volume 2 of 2


Module 3 - Geometry

-Explanation- This module describes the basic geometric figures of triangles, quadrilaterals, and circles; and the calculation of area and volume.

 

 

 

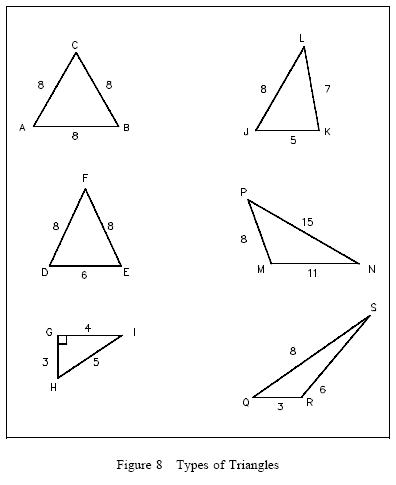
Triangles

 

A triangle is a figure formed by using straight line segments to connect three points that are not in a straight line. The straight line segments are called sides of the triangle.

Examples of a number of types of triangles are shown in Figure 8. An equilateral triangle is one in which all three sides and all three angles are equal. Triangle ABC in Figure 8 is an example of an equilateral triangle. An isosceles triangle has two equal sides and two equal angles (triangle DEF). A right triangle has one of its angles equal to 90° and is the most important triangle for our studies (triangle GHI). An acute triangle has each of its angles less than 90° (triangle JKL). Triangle MNP is called a scalene triangle because each side is a different length. Triangle QRS is considered an obtuse triangle since it has one angle greater than 90°. A triangle may have more than one of these attributes. The sum of the interior angles in a triangle is always 180°.

 

 

 

 

 

 

 

 

 

 

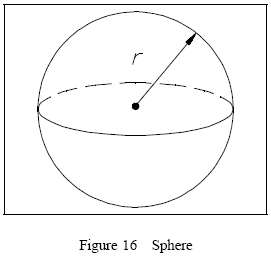
Sphere

A sphere is a solid, all points of which are equidistant from a fixed point, the center, as shown in Figure 16.

The volume of a sphere is calculated using the following formula:

        V =4/3ðr3                                                         (3-15)

The surface area of a sphere is calculated using the following formula:

       SA = 4ðr2                                                          (3-16)

 

 

 

 

 

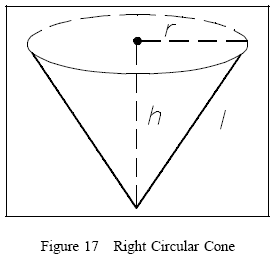
Right Circular Cone

A right circular cone is a cone whose axis is a line segment joining the vertex to the midpoint of the circular base, as shown in Figure 17.

The volume of a right circular cone is calculated using the following formula:

V = 1/3ðr2h                                                   (3-17)

The surface area of a right circular cone is calculated using the following formula:

SA = ðr2 + ðrl                                               (3-18)

 

 

 

 

 

BASIC CONCEPTS OF GEOMETRY

Terms

Lines
Important Facts
Angles
Summary

SHAPES AND FIGURES OF PLANE GEOMETRY

Triangles
Area and Perimeter of Triangles
Quadrilaterals
Circles

Summary

SOLID GEOMETRIC FIGURES

Rectangular Solids
Cube
Sphere
Right Circular Cone
Right Circular Cylinder
Summary

Module 4 - Trigonometry

-Explanation- This module describes the trigonometric functions of sine, cosine, tangent, cotangent, secant, and cosecant. The use of the Pythagorean theorem is also discussed.

 

 

 

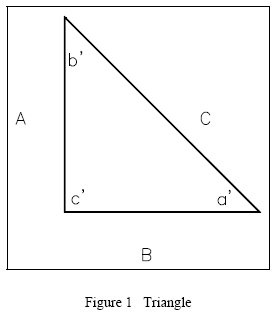
Pythagorean Theorem

 

The Pythagorean theorem is a tool that can be used to solve for unknown values on right triangles. In order to use the Pythagorean theorem, a term must be defined. The term hypotenuse is used to describe the side of a right triangle opposite the right angle. Line segment C is the hypotenuse of the triangle in Figure 1. The Pythagorean theorem states that in any right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides.

This may be written as c2 = a2 + b

 

 

 

 

 

PYTHAGOREAN THEOREM

Pythagorean Theorem
Summary

TRIGONOMETRIC FUNCTIONS

Inverse Trigonometric Functions
Summary

RADIANS

Radian Measure
Summary

Module 5 - Higher Concepts of Mathematics

-Explanation- This module describes logarithmic functions, statistics, complex numbers, imaginary numbers, matrices, and integral and derivative calculus.

 

 

 

 

 

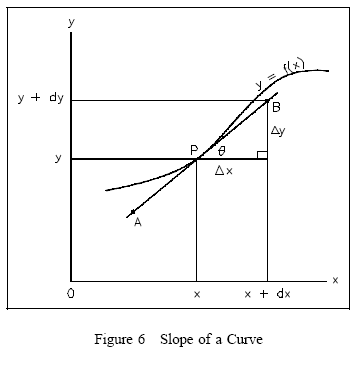
When the graph of a function is not a straight line, the slope of the plot is different at different points. The slope of a curve at any point is defined as the slope of a line drawn tangent to the curve at that point. Figure 6 shows a line drawn tangent to a curve. A tangent line is a line that touches the curve at only one point. The line AB is tangent to the curve y = f(x) at point P.

 

 

 

 

 

 

 

 

 

 

Integrals and Summations in Physical Systems

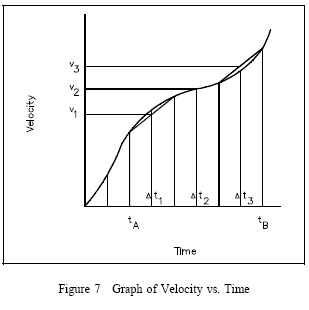
Differentials and derivatives arose in physical systems when small changes in one quantity were considered. For example, the relationship between position and time for a moving object led to the definition of the instantaneous velocity, as the derivative of the distance traveled with respect to time, ds/dt. In many physical systems, rates of change are measured directly. Solving problems, when this is the case, involves another aspect of the mathematics of dynamic systems; namely integral and summations.

Figure 7 is a graph of the instantaneous velocity of an object as a function of elapsed time. This is the type of graph which could be generated if the reading of the speedometer of a car were recorded as a function of time.

 

 

 

 

 

 

 

 

STATISTICS

Frequency Distribution
The Mean
Variability
Normal Distribution
Probability
Summary

IMAGINARY AND COMPLEX NUMBERS

Imaginary Numbers
Complex Numbers
Summary

MATRICES AND DETERMINANTS

The Matrix
Addition of Matrices
Multiplication of a Scaler and a Matrix
Multiplication of a Matrix by a Matrix
The Determinant
Using Matrices to Solve System of Linear Equation
Summary

CALCULUS

Dynamic Systems
Differentials and Derivatives
Graphical Understanding of Derivatives
Application of Derivatives to Physical Systems
Integral and Summations in Physical Systems
Graphical Understanding of Integral
Summary

 

 

 

 

DOE Fundamentals Handbook - Mathematics $17.95

 

 

 

The Mathematics handbook includes a review of introductory mathematics (i.e. addition, subtraction, multiplication and division involving whole numbers, decimals, fractions, exponents and radicals) and the concepts and functional use of algebra, geometry, trigonometry and calculus. Word problems, equations, calculations and practical exercises that require the use of each of the mathematical concepts are also presented. This book will provide YOU with a foundation for performing basic mathematical calculations and understanding the significance of things like quadratic equations, the Pythagorean Theorem, logarithms and trigonometric functions of sine, cosine, tangent, cotangent, secant and cosecant.
The Mathematics handbook presents more than enough information to provide the reader with a fundamental knowledge level sufficient to understand advanced theoretical concepts presented in many other subject areas, including all of the sciences, statistical use of data and all those other realms of life that our parents and teachers told us way back when that we would need math for some day… This book is a Godsend for undergraduate students preparing for the GRE’s who are in desperate need of a wonderfully clear, concise and FUNDAMENTAL breakdown of mathematics. It is also particularly useful for anyone in any field that finds their math skills woefully inadequate or even just rusty to the point of irritation